CÁLCULO DIFERENCIAL E INTEGRAL I
Dada a função y = x5/2 assinale a alternativa CORRETA que representa a sua primeira derivada.
(5/2)x3/2
(3/2)x3/2
(5/2)x3/4
(5/2)x1/2
(4/3)x3/2
Dada a função f: R -> R definida por f(x) = x2/3 , assinale a alternativa CORRETA que representa a sua primeira derivada.
(3/2)x1/3
(2/3)x-1/3
(2/3)x1/3
(3/2)x-1/3
(2/3)x-2/3

8
11
10
9
7

324
184
234
243
124
A equação horária de um corpo em movimento é dada por s(t)=t3. Calcule a velocidade do corpo num instante t qualquer. Assinale a alternativa correta referente a velocidade no instante de t=4s.
9
28
38
18
48
Observe o gráfico, a seguir representado:
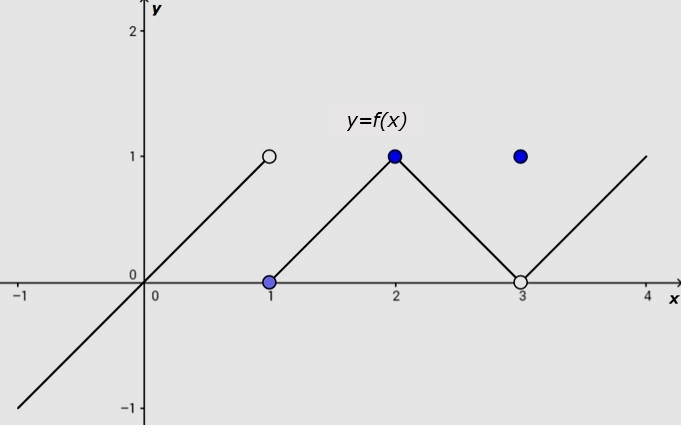
Ao observar o gráfico é possível afirmar que:
I) ( ) O limite da função quando x tende 0 (zero) é igual a 0 (zero).
II) ( ) O limite da função quando x tende a 2 (dois) é igual a 1 (um).
III) ( ) O limite da função quando x tende a 3 (três) não existe, pois os limites laterais são diferentes.
IV) ( ) O limite da função quando x tende a 1 (um) não existe, pois os limites laterais são diferentes.
V) ( ) O limite da função é sempre igual a 1 (um) em qualquer ponto de tendência.
Assinale a alternativa CORRETA:
II, III e IV apenas
I e III e V apenas
II, IV e V apenas
I, II e IV apenas.
I, II, III e IV apenas
Assinale a alternativa correta da derivada :

(5/2)x3/2
(3/2)x3/2
(5/2)x3/4
(5/2)x1/2
(4/3)x3/2
Dada a função f: R -> R definida por f(x) = x2/3 , assinale a alternativa CORRETA que representa a sua primeira derivada.
(3/2)x1/3
(2/3)x-1/3
(2/3)x1/3
(3/2)x-1/3
(2/3)x-2/3

8
11
10
9
7

324
184
234
243
124
A equação horária de um corpo em movimento é dada por s(t)=t3. Calcule a velocidade do corpo num instante t qualquer. Assinale a alternativa correta referente a velocidade no instante de t=4s.
9
28
38
18
48
Observe o gráfico, a seguir representado:

Ao observar o gráfico é possível afirmar que:
I) ( ) O limite da função quando x tende 0 (zero) é igual a 0 (zero).
II) ( ) O limite da função quando x tende a 2 (dois) é igual a 1 (um).
III) ( ) O limite da função quando x tende a 3 (três) não existe, pois os limites laterais são diferentes.
IV) ( ) O limite da função quando x tende a 1 (um) não existe, pois os limites laterais são diferentes.
V) ( ) O limite da função é sempre igual a 1 (um) em qualquer ponto de tendência.
Assinale a alternativa CORRETA:
II, III e IV apenas
I e III e V apenas
II, IV e V apenas
I, II e IV apenas.
I, II, III e IV apenas
Assinale a alternativa correta da derivada :

(3/2)x1/3
(2/3)x-1/3
(2/3)x1/3
(3/2)x-1/3
(2/3)x-2/3

8
11
10
9
7

324
184
234
243
124
A equação horária de um corpo em movimento é dada por s(t)=t3. Calcule a velocidade do corpo num instante t qualquer. Assinale a alternativa correta referente a velocidade no instante de t=4s.
9
28
38
18
48
Observe o gráfico, a seguir representado:

Ao observar o gráfico é possível afirmar que:
I) ( ) O limite da função quando x tende 0 (zero) é igual a 0 (zero).
II) ( ) O limite da função quando x tende a 2 (dois) é igual a 1 (um).
III) ( ) O limite da função quando x tende a 3 (três) não existe, pois os limites laterais são diferentes.
IV) ( ) O limite da função quando x tende a 1 (um) não existe, pois os limites laterais são diferentes.
V) ( ) O limite da função é sempre igual a 1 (um) em qualquer ponto de tendência.
Assinale a alternativa CORRETA:
II, III e IV apenas
I e III e V apenas
II, IV e V apenas
I, II e IV apenas.
I, II, III e IV apenas
Assinale a alternativa correta da derivada :

8
11
10
9
7

324
184
234
243
124
A equação horária de um corpo em movimento é dada por s(t)=t3. Calcule a velocidade do corpo num instante t qualquer. Assinale a alternativa correta referente a velocidade no instante de t=4s.
9
28
38
18
48
Observe o gráfico, a seguir representado:

Ao observar o gráfico é possível afirmar que:
I) ( ) O limite da função quando x tende 0 (zero) é igual a 0 (zero).
II) ( ) O limite da função quando x tende a 2 (dois) é igual a 1 (um).
III) ( ) O limite da função quando x tende a 3 (três) não existe, pois os limites laterais são diferentes.
IV) ( ) O limite da função quando x tende a 1 (um) não existe, pois os limites laterais são diferentes.
V) ( ) O limite da função é sempre igual a 1 (um) em qualquer ponto de tendência.
Assinale a alternativa CORRETA:
II, III e IV apenas
I e III e V apenas
II, IV e V apenas
I, II e IV apenas.
I, II, III e IV apenas
Assinale a alternativa correta da derivada :

324
184
234
243
124
A equação horária de um corpo em movimento é dada por s(t)=t3. Calcule a velocidade do corpo num instante t qualquer. Assinale a alternativa correta referente a velocidade no instante de t=4s.
9
28
38
18
48
Observe o gráfico, a seguir representado:

Ao observar o gráfico é possível afirmar que:
I) ( ) O limite da função quando x tende 0 (zero) é igual a 0 (zero).
II) ( ) O limite da função quando x tende a 2 (dois) é igual a 1 (um).
III) ( ) O limite da função quando x tende a 3 (três) não existe, pois os limites laterais são diferentes.
IV) ( ) O limite da função quando x tende a 1 (um) não existe, pois os limites laterais são diferentes.
V) ( ) O limite da função é sempre igual a 1 (um) em qualquer ponto de tendência.
Assinale a alternativa CORRETA:
II, III e IV apenas
I e III e V apenas
II, IV e V apenas
I, II e IV apenas.
I, II, III e IV apenas
Assinale a alternativa correta da derivada :

9
28
38
18
48
Observe o gráfico, a seguir representado:

Ao observar o gráfico é possível afirmar que:
I) ( ) O limite da função quando x tende 0 (zero) é igual a 0 (zero).
II) ( ) O limite da função quando x tende a 2 (dois) é igual a 1 (um).
III) ( ) O limite da função quando x tende a 3 (três) não existe, pois os limites laterais são diferentes.
IV) ( ) O limite da função quando x tende a 1 (um) não existe, pois os limites laterais são diferentes.
V) ( ) O limite da função é sempre igual a 1 (um) em qualquer ponto de tendência.
Assinale a alternativa CORRETA:
II, III e IV apenas
I e III e V apenas
II, IV e V apenas
I, II e IV apenas.
I, II, III e IV apenas
Assinale a alternativa correta da derivada :


II, III e IV apenas
I e III e V apenas
II, IV e V apenas
I, II e IV apenas.
I, II, III e IV apenas